Explanation of the gravitation presuming neutrino medium

Laszlo István Orbán and László Tihamér Orban

 

1. STATIC GRAVITATION FIELD

Although gravitation was the first of the four basic interactions that science started to examine, still utmost attention is paid to experimental or theoretical research that aims to better understand the fundamentals of the gravitation. Here the authors would like to present a theoretical method that establishes relationship between the gravitation force and the cosmic neutrinos.

 

Let us first assume that the neutrinos that have finite rest masses, - this has been proved already through experiments - can be found everywhere and are evenly distributed in the Universe. According to this assumption, this medium consists of chaotic moving free neutrinos. The only possible interaction among them is the elastic collision.

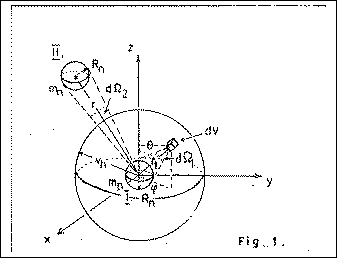
Let assume that the gravitation effect is conveyed between two objects by the above mentioned neutrino medium. Thus, at the calculation of the gravitation force between these objects, one must determine the number of the neutrino that interacts with both objects, and the impulse variation transported by these neutrinos. The calculations are related to the unit of time.

 

Let discuss the case of two macroscopic objects with masses m₁ and m₂ that are separated by a distance r from each other.

These bodies at lowest level are composed by microscopic particles with the mass m_n and radius R_n.

The neutrinos will interact with the microscopic particles around them, hence the sum of the micro-effects will result a macroscopic effect.
Let us first determine the number of medium-elements making interaction during the time-unit within a spherical microelement having the radius R_n (see Fig 1).

From the Fig.1 it can be concluded that only those dN₁ neutrinos - within the dN number of medium elements being in a dV volume - can make interaction with the sphere I that have the direction of their velocity vector falling inside the solid angle d Q₁.
The ratio between the solid angles will be equal to the ratio of the corresponding neutrino numbers since the evenly distributed medium elements are in continuous chaotic motion. Thus one can write:

4 p	=	dN
d WI		dN I

from which results:

dNI  =	d WI
		dN
	4 p

where 4p is the value of the total solid angle in sterradian.

By definition,

dW1   =	pRn2
	r12

Introducing the notation

r N	=	dN
		dV

which represents the density of the elements (number of medium elements / volume), one can write:

dNI   =	p Rn2	rn dV	=	Rn2 rn	dV
	r12	4 p		4r12

The total number of the elements in the medium (  N₁  ) interacting in the time-unit with the sphere of radius R_n, can be obtained by summarizing the dN values contained in each sphere with the radius v _h this will result the integral below:

NI   =			dV   =		2 p	p	vh
		r N  RN2		r N  RN2				rI2  sin Q1  drI  d Q1  d j
									=
		4rI2		4				rI2
					0	0	R

  =   p r _N   R_n² ( v_h - R_n )

where v_h is the propagation velocity of the wave in the medium. Presuming this environment behaves similar to all the elastic mediums, one can write: 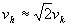; where   v_h stands for the propagation velocity of the interactions in the given medium; while   v_k stands for the mean value of the velocity for medium-elements.

The expression of the previous integral:

N₁ = p r_N R_n² ( v_h - R_n )

can be simplified if   v_n >> R_n   thus:

N₁ » p r _N R _n² v_h

Lets annotate the microscopic particles mass with   m_n   and its radius with   R_n.
From the medium-particles ( N₁ ) that collides with the sphere I., only those ( N₂ ) will collide with the sphere II. that have their velocity vector pointing toward the solid angle having the value:

d W 2 =	p Rn2
	r2

This deduction was based on the assumption that the neutrinos reflected from the sphere I. got in the neighborhood of sphere II. in a straight line, but in the reality due to numerous collisions, they make a zigzag path. When two medium-particles of identical masses have elastic impacts, it can be assumed that because of the changes in the velocities the particle a will continue to travel in straight direction. The ratio of the solid angles – similar to the previous case - will be equal to the ratio between the numbers of medium-elements:

4 p	=	N1
d W		N2

from which

N2 =	d W 2	N1
	4 p

After performing the substitution the expression for N₂ will be:

N2 =	p Rn2	p r N Rn2 vh   =	p	r N Rn4 vh	1
	4 p   r2		4		r2

Let us replace the I. and II. micro objects with the m1 and m2 macroscopic bodies. The value of total collisions in the first approximation can be estimated as the number of collisions multiplied with the number of elementary particles the macroscopic bodies is built up.
This is valid for the so-called weak gravitation fields, where the size of macroscopic bodies is much less then the distance traveled by the wave in the unit of time. Furthermore the self-dashing effect can be neglected that would appear for the particles building up the macroscopic object.
The number of particles for the macroscopic part object be calculated as the ratio between m₁ /m_n and m₂ /m_n. Therefore the N₁ and N₂ values should be multiplied with these values. Thus the numbers of neutrinos (N_1,2) that make interaction between the two macroscopic bodies can be given by:

N1,2 =	m1	m2	p	r N Rn4 vh	1	=	p r N Rn4 vh	m1 m2
	mn	mn	4		r2		4 mn2	r2

Finally the gravitational force will be obtained by multiplying the N_1,2 with the sum of impulse-variations resulting from the collision between the neutrinos and the I. and II. macroscopic objects. Let calculate this value. Presuming a elastic collision between the neutrinos and the static microscopic particles, the velocity of the medium-element after collision would be:

u1 =	mn - mk	vk
	mn + mk

where m_k is the mass and v_k the velocity of the neutrino, whereas the m_n is the mass of the microscopic particle.

The D p impulse variation of the medium element can be written as:

D p = mk vk - mk u1 = mk ( vk -	mn - mk	vk ) =	2 mk2 vk
	mn + mk		mn + mk

If m_n > > m_k and 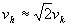, then

D p = 2	mk2 vh
	mn

and the force F measured between the macroscopic bodies is:

(1).		F = N1,2 D p =	p  r N Rn4 vh	m1 m2	2 mk2 vh	=	p	r N mk2 Rn4 vh2	m1 m2
			4 mn2	r2	mn			mn3	r2

that means:

(2)                                                             
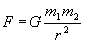
                                          if
(3)                                                             

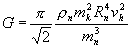
The formula obtained is Newton's gravitation law for the case of weak gravitation fields. Based on the formula (3), the gravitation constant G can be determined through the properties of the neutrino medium and the particles that builds up the macroscopic objects.

It comes out from the presented deduction that a certain time is needed to convey the gravitation force between the objects. This time is determined by the speed of medium elements and the distance between the objects. Furthermore can be concluded that gravitation waves are generated whenever an object makes periodic or accelerating movement in the neutrino medium. Consequently, the gravitation effects and the gravitation waves are supposed to be transferred by the medium consisting from neutrinos.

A proof of this theory would be if substituting the experimental values into the formula the constant value  G = 6.67·10^-11 Nm²/kg² be obtained for the gravitational constant.
At this moment this issue cannot be determined so easily since there are no reliable data about the cosmic neutrinos. Furthermore it is not determined yet whether nucleons, pions, quarks, gluons or leptons can be used as parameters for m_n and R_n in the previous formula calculating G. It would be important to determine which neutrinos (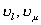' 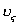) the medium consist of. It would be essential also to find out if the medium's wave velocity (v_h) is equal with the speed of the light or differs from it.

Based on various experiments, the neutrino's mass is less then 17 eV » 3·10^-35 kg. Using this value, and supposing that v_h = c , the density values
r _N  and   r  = r _N m_k could be determined from the following formula:

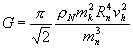
The calculation was carried out with different m_m and R_m values ( see Table I. )

Table I : Estimation for the density of the neutrino medium

Elementary particle in bodies	mn kg	Rn m	G Nm2kg-2	mk kg	vh ms-1	rN part/m3	r kg/m3
Nucleons (protons, neutrons)	1.67·10-27	10-15	6.67·10-11	3·10-35	3·108	1.72·1021	5.18·10-14
Pions	2.5·10-28	10-16	6.67·10-11	3·10-35	3·108	5.79·1022	1.74·10-12
Quark	5.88·10-28	10-16	6.67·10-11	3·10-35	3·108	7.54·1023	2.26·10-11
Lepton	9.1·10-31	2.8·10-15	6.67·10-11	3·10-35	3·108	4.54·109	1.36·10-25

From the data-table above the value r » 1.36·10^-25 kg m^-3 seems to be the most realistic one.
This value is the closest to the limit density 4.5 10^-27 kg m^-3, which predicts the expansion or contraction of the Universe.
If the experiments will confirm the existence of the neutrino medium with the density of r » 10^-25 kg m^-3. then the gravitation force may be interpreted as the result of interactions between the neutrinos and electrons. Any other approach would give a density value higher with 11-14 magnitudes.

2. THE  "GRAVO-DYNAMIC"  FORCE

Assuming the existence of neutrino medium, the shift of matter (flux of substance) may result forces similar to the magnetic forces generated by electric currents. This gravo-dynamic force should be extremely weak for speeds negligible in comparison with the speed of the light. Therefore the gravo-dynamic effects may be perceptible only on the cosmic scale having mass fluxes in the range of galaxies and cluster of galaxies.

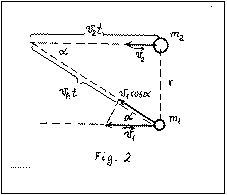
Let suppose that two bodies  m₁  and m₂ are moving in parallel at the speeds  v₁  and v₂. If v₁ and v₂ are negligible in comparison with v_h then only the transferred impulse-variation has to be recalculated since N_1,2, (in the first approximation) will be identical with those calculated in the static case.

The medium element will collide with  m₁  and  m₂  if:

v_h² t² = r² + v₂² t²,

then

cos a  =	v2 t	=	v2
	vh t		vh

Those medium-elements will collide with the particle with mass m₁, that are moving with the speed given by the expression v₁cos a.
The velocity u_1,1 of the medium-element (supposing elastic collision) after the collision can be calculated from the energy and impulse conservation laws.

u1,1 =	2 mn v1 cos a   + (mn - mk) vk
	mn + mk

The sum of the impulse variations transferred by the medium elements:

D p = m_k ( v_k - u_1,1 ) =

= mk ( vk -	mn - mk	vk -	2 mn v1 cos a	) =	mk	(2 mk vk - 2 mn v1 cos a )
	mn + mk		mn + mk		mn + mk

Substituting the

cos a =	v2
	vh

into the previous expression the expression will look like

D p =	2 mk2 vk	=	2 mn mk	v1 v2
	mn + mk		mn + mk	vh

If m_n > m_k and 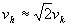then

D p =	2 mk2 vh	-	2 mk v1 v2
	mn		vh

The force between two moving bodies can be calculated also with the formula: F = N_1,2 Dp that will result:

F =	p	r N vh2 mk2 Rn4	m1 m2	-	p	r N mk Rn4	m1 v1 m2 v2
		mn3	r2		2	mn2	r2

From the expression 3 and the above deducted formula one can have:

Gd =	p	r N mk2 Rn4	=	1	mn	G
	2	mn2			mk vh2

Then one can get:

F = G	m1 m2	-   Gd	m1 v1 m2 v2	=  Fs   -   Fd
	r2		r2

According to this formula, in addition to the static force ( F_s ) an additional, speed dependent dynamic force ( F_d ) will also arise.

Replacing the   m₁ v₁   with   I₁  Dl₁ and   m₂ v₂   with   I₂  Dl₂ , the gravo-dynamic force will have the form very similar to the electro-dynamics force.

Fd   =   Gd	I1  D l1   I2  D l2
	r2

Where,   I₁   and   I₂ are the “mass-current-intensities" , whereas   D l₁   and   D l₂   are the elementary segments in the space.

In the general case, when the vectors   D l₁   and   D l₂   have different angles with the   r   distance vector, the gravo-dynamic vector-force is calculated as a vector-product:

Fd   =   Gd I1 I2	( D l1 x r )   x   D l2
	r3

One can understand that in the case of moving objects, addition to the static gravitation field a dynamic field will also arise. The description of the dynamic gravitational (gravo-dynamic) field can be done similar to the electro-dynamic field. However while in the electro-dynamic case the   ( I )   means electric current, in the case of gravo-dynamic force would mean mass-current-intensity whereas instead of permeability used in the electro-dynamic case one will use the gravitational constant G_d.

Since the relation between   G_d   and   G   can be given by the formula:

Gd   =	1	mn	G
		mk vh2

As long as the numeric values for   v₁   and   v₂   are very small in comparison with   v_h   ( v₁ , v₂ << v_h ), the “gravo-dynamic” force can be neglected in comparison with the static gravitational force. In addition, while the value of the   m_n / m_k   ratio is uncertain, further research is expected on this field.

Finally, let us emphasize that the assumption of neutrino field enables both to predict the gravitational effects and helps to better understand many other phenomenon of the quantum physics.